Poverty analysis as a partial equilibrium exercise

economics ▪ policy ▪

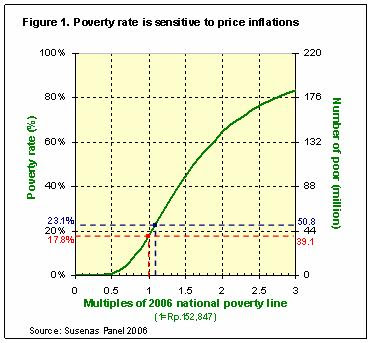
Rasyad Parinduri argues here that Figure 1 of this article (shown below), to quote him, "cannot tell us 'how sensitive the poverty rate is to increases in the poverty line'" because it doesn't plot the poverty rate against the poverty line. I'll try to explain here why he's wrong by drawing an analogy to the supply-demand curve familiar to most undergraduate economics student.



[PS: My apology to those not familiar with the demand and supply curves since this post may be a bit arcane.]
But first, what are demand and supply curves? A demand curve simply traces the number of people willing to pay for a certain good at a certain price. The supply curve, on the other hand, traces the number of people willing to produce a certain good given a certain price paid for it. Both supply and demand curves trace two variables: the number of people and the price observed (for one, the buying price; for another, the selling price). This is Microeconomics 101.



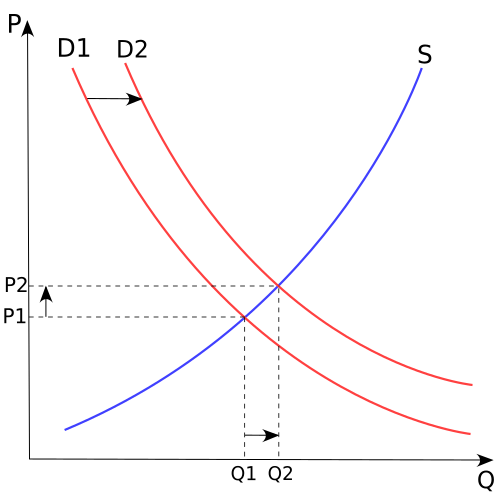
The graph above are supply and demand curves. The point at which the two curves intersect is what we call the equilibrium (price-quantity) point. Given the population's demand and supply curves, this equilibrium point describes the price and quantity at which goods are actually traded in a competitive market. Shifts in the either curve can change this equilibrium point (or the actual price/quantity-exchanged observed in the market).

How is the poverty graph analogous to the supply-demand graph? First, the axes. The poverty graph plots the number of people against the expenditure level. It is actually almost like a supply-demand graph with former variable analogous to quantity; the latter, price; and the axes reversed (that is, instead of having Q(uantity) on the x-axis, the "quantity" in the poverty graph is now on the y-axis -- and vice versa).

Second, the curves. The way I draw it, the green curve (an expenditure cumulative distribution function or cdf) traces the number of people whose income are below the expenditure level shown on the x-axis. At a higher the expenditure level, the number of people below this income increases. I'll call this "the expenditure distribution curve" and it's behaviour is a bit like the supply curve.

Now, the poverty line is a bit tricky -- it's not exactly analogous to the demand curve. The poverty line is that expenditure level where people subsist. For simplicity, most analyses draw the poverty line as a straight vertical line, but in reality, it probably isn't. Depending on one's characteristics (geographical location, choice of food, even biological metabolisms), this level (converted into expenditure levels) may differ for each individual. The actual poverty line is not smooth, but the (fitted) curve is likely to be almost vertical will definitely cut the expenditure distribution curve. In a way, the poverty line is analogous an administered producer price in the supply-demand context.

So, the curves aren't really analogous to the supply-demand curves (since there is no analogy to the demand curve). But what is important is the fact that the actual poverty rate that we observe comes from the intersection of these two curves, just like the actual price/quantity combination we observe comes from the intersection of the supply and demand curves. Each individual curve does not have adequate information to tell us about the actual poverty rate, just like the supply curve (or the demand curve) alone cannot tell us the actual price we will observe in the market. I thing, this is the point that Rasyad missed.

Supply-demand graphs are used all the time to explain the sensitivity of equilibrium quantity to changes in administered prices in a partial equilibrium sense -- that is, under the assumption that the change in the administered price did not change the behaviour of the supply curve (what economists call "ceteris paribus"). It is exactly in this ceteris paribus manner that the above poverty graph should be used to elaborate the effect of the change in poverty line to the poverty rate.